Bitwise operators — Facts and Hacks
Bitwise operators are operators (just like &, |, << etc.) that operate on ints and uints at the binary level. This means they look directly at the binary digits or bits of an integer. This all sounds scary, but in truth bitwise operators are quite easy to use. They are really fast as compared to other programming techniques because these operations are carried out directly by the processor. So you should have a good understanding of these and how to use them they are quite often asked in interviews. So let’s have a look how these tiny operators can save our time.
This article seems so large but it is quite easy to understand. Also if you are familiar with the Bitwise operator then you can skip directly to Bitwise Hack section.
There are 6 Bitwise operators namely:
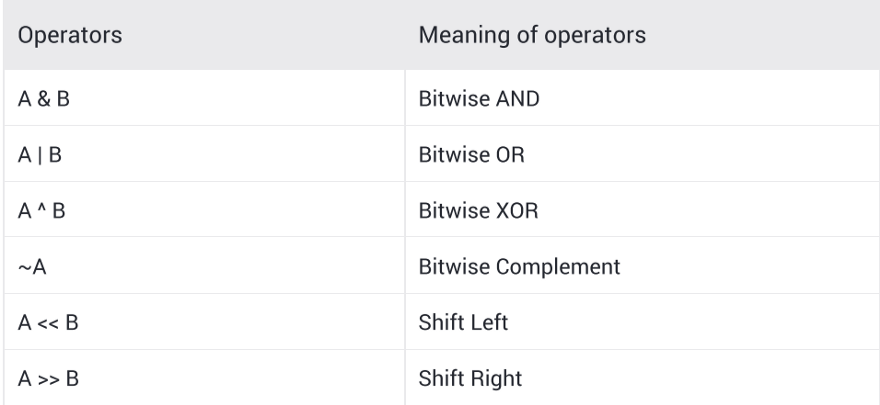
And some more created by there combinations, some of them are listed here:
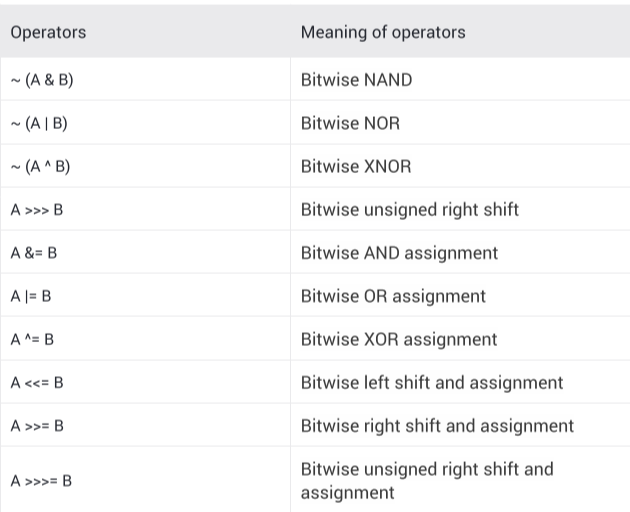
Let’s go through the six bitwise operators one by one (or you can directly skip to facts)
Bitwise AND operator &
The output of bitwise AND is 1 if the corresponding bits of two operands is 1. If either bit of an operand is 0, the result of corresponding bit is evaluated to 0.
Let us suppose the bitwise AND operation of two integers 12 and 25.
12 = 00001100 (In Binary) 25 = 00011001 (In Binary) Bit Operation of 12 and 25 00001100 & 00011001 ________ 00001000 = 8 (In decimal)
Example Code
int main()
{
int a = 12, b = 25;
printf(“Output = %d”, a&b);
return 0;
}
Output = 8
Bitwise OR operator |
The output of bitwise OR is 1 if at least one corresponding bit of two operands is 1. In C Programming, bitwise OR operator is denoted by |.
12 = 00001100 (In Binary) 25 = 00011001 (In Binary) Bitwise OR Operation of 12 and 25 00001100 | 00011001 ________ 00011101 = 29 (In decimal)
Example Code
int main()
{
int a = 12, b = 25;
printf("Output = %d", a|b);
return 0;}
Output = 29
Bitwise XOR (exclusive OR) operator ^
The result of bitwise XOR operator is 1 if the corresponding bits of two operands are opposite. It is denoted by ^.
XOR is used in solving a large number of questions
12 = 00001100 (In Binary) 25 = 00011001 (In Binary) Bitwise XOR Operation of 12 and 25 00001100 | 00011001 ________ 00010101 = 21 (In decimal)
Example Code
int main()
{
int a = 12, b = 25;
printf("Output = %d", a^b);
return 0;
}
Output = 21
The bitwise XOR operator is the most useful operator from technical interview perspective. It is used in many problems. A simple example could be “Given a set of numbers where all elements occur even number of times except one number, find the odd occurring number” This problem can be efficiently solved by just doing XOR of all numbers.
// Function to return the only odd occurring element
int findOdd(int arr[], int n) {
int res = 0, i;
for (i = 0; i < n; i++)
res ^= arr[i];
return res;
}
int main(void) {
int arr[] = {12, 12, 14, 90, 14, 14, 14};
int n = sizeof(arr)/sizeof(arr[0]);
printf ("The odd occurring element is %d ", findOdd(arr, n));
return 0;
}
// Output: The odd occurring element is 90
The following are many other interesting problems which can be used using XOR operator. Find the Missing Number, swap two numbers without using a temporary variable, A Memory Efficient Doubly Linked List, and Find the two non-repeating elements. There are many more (See this, this, this, this, this and this)
Bitwise complement operator ~
Bitwise compliment operator is an unary operator (works on only one operand). It changes 1 to 0 and 0 to 1. It is denoted by ~.
35 = 00100011 (In Binary) Bitwise complement Operation of 35 ~ 00100011 ________ 11011100 = 220 (In decimal)
Twist in bitwise complement operator in C Programming
The bitwise complement of 35 (~35) is -36 instead of 220, but why?
For any integer n, bitwise complement of n will be -(n+1). But why?
This is because in integers the first bit is used for determining the sign of the number (+ve/-ve). Hence for uint simply convert the flipped number to decimal to get the compliment (220 in this case).
But for integer first digit gets reversed which changes the sign and hence the number can be calculated by converting rest of the bits to decimal with a negative sign (or positive in case of negative compliment).
For simplicity 2’s compliment of the flipped digit is calculated which gives us the result. An example is shown below.
2’s Complement
Two’s complement is an operation on binary numbers. The 2’s complement of a number is equal to the complement of that number plus 1. For example:
Decimal Binary 2’s complement
0 00000000 -(########+1) = -00000000 = -0(decimal) 1 00000001 -(####1110+1) = -######## = -256(decimal) 12 00001100 -(####0011+1) = -####0100 = -244(decimal) 220 11011100 -(00100011+1) = -00100100 = -36(decimal)
Note: Overflow is ignored while computing 2’s complement.
The bitwise complement of 35 is 220 (in decimal). The 2’s complement of 220 is -36. Hence, the output is -36 instead of 220.
Bitwise complement of any number N is -(N+1). Here’s how:
bitwise complement of N = ~N (represented in 2’s complement form)
2’complement of ~N= -(~(~N)+1) = -(N+1)
Example Code
int main()
{
printf(“complement = %d\n”,~35);
printf(“complement = %d\n”,~-12);
return 0;
}
Output
complement = -36
Output = 11
Right Shift Operator
Right shift operator shifts all bits towards right by certain number of specified bits. It is denoted by ».
If we’re starting with a negative number (a binary number where the leftmost bit is a 1), all the empty spaces are filled with a 1. If we’re starting with a positive number (where the leftmost bit, or most significant bit, is a 0), then all the empty spaces are filled with a 0. Again, this all goes back to two’s complement.
While this sounds complicated, it basically just preserves the sign of the number we start with. So -8 » 2 == -2 while 8 » 2 == 2. I’d recommend trying those out on paper yourself.
212 = 11010100 (In binary) 212>>2 = 00110101 (In binary) [Right shift by two bits] 212>>7 = 00000001 (In binary) 212>>8 = 00000000 212>>0 = 11010100 (No Shift)
Left Shift Operator
Left shift operator shifts all bits towards left by certain number of specified bits. It is denoted by «.
Of course! Any empty spots are just replaced with 0s. And that’s all there is to the left bitshift. Keep in mind that Flash always thinks the result of a left bitshift is an int, not a uint. So if you need a uint for some reason, you’ll have to cast it to a uint like this: uint(37 « 3). This casting doesn’t actually change any of the binary information, just how Flash interprets it (the whole two’s complement thing).
212 = 11010100 (In binary) 212<<1 = 110101000 (In binary) [Left shift by one bit] 212<<0 =11010100 (Shift by 0) 212<<4 = 110101000000 (In binary) =3392(In decimal)
Example Code
int main()
{
int num=212, i;
for (i=0; i<=2; ++i)
printf(“Right shift by %d: %d\n”, i, num>>i);
printf(“\n”);
for (i=0; i<=2; ++i)
printf(“Left shift by %d: %d\n”, i, num<<i);
return 0;
}
Output
Right Shift by 0: 212
Right Shift by 1: 106
Right Shift by 2: 53
Left Shift by 0: 212
Left Shift by 1: 424
Left Shift by 2: 848
The »> Operator
Our final bitwise operator is the bitwise unsigned right shift. This is very similar to the regular bitwise right shift, except that all empty bits on the left are filled with 0s. This means the result of this operator is always a positive integer and it always treats the integer being shifted as an unsigned integer. We won’t run through an example of this in this section, but we’ll see a use for it very shortly.
Bit shifts
The bit shift operation can be done in 4 ways discussed below. These are not so important by interview point of view and are never asked but yes quite simple to remember even by looking at the names you will get a hint of their operation.
Arithmetic shift
These are simply the left and right shifts discussed earlier.
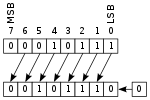
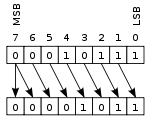
Logical shift
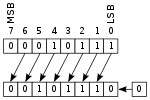
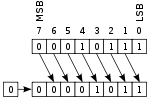
In a logical shift, zeros are shifted in to replace the discarded bits. Therefore, the logical and arithmetic left-shifts are exactly the same.
However, as the logical right-shift inserts value 0 bits into the most significant bit, instead of copying the sign bit, it is ideal for unsigned binary numbers, while the arithmetic right-shift is ideal for signed two’s complement binary numbers.
Circular shift
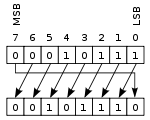
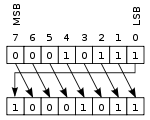
Another form of shift is the circular shift or bit rotation. In this operation, the bits are “rotated” as if the left and right ends of the register were joined. The value that is shifted in on the right during a left-shift is whatever value was shifted out on the left, and vice versa. This operation is useful if it is necessary to retain all the existing bits, and is frequently used in digital cryptography.
Rotate through carry
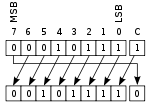
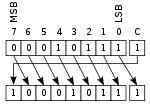
Rotate through carry is similar to the rotate no carry operation, but the two ends of the register are separated by the carry flag. The bit that is shifted in (on either end) is the old value of the carry flag, and the bit that is shifted out (on the other end) becomes the new value of the carry flag.
A single rotate through carry can simulate a logical or arithmetic shift of one position by setting up the carry flag beforehand. For example, if the carry flag contains 0, then x RIGHT-ROTATE-THROUGH-CARRY-BY-ONE is a logical right-shift, and if the carry flag contains a copy of the sign bit, then x RIGHT-ROTATE-THROUGH-CARRY-BY-ONE is an arithmetic right-shift. For this reason, some microcontrollers such as low end PICs just have rotate and rotate through carry, and don’t bother with arithmetic or logical shift instructions.
Rotate through carry is especially useful when performing shifts on numbers larger than the processor’s native word size, because if a large number is stored in two registers, the bit that is shifted off the end of the first register must come in at the other end of the second. With rotate-through-carry, that bit is “saved” in the carry flag during the first shift, ready to shift in during the second shift without any extra preparation.
Mathematical equivalents:
For the mathematics enthusiast here are the mathematical representation of these bitwise operators:
Assuming x ≥ y, for the non-negative integers, the Bitwise operations can be written as follows:
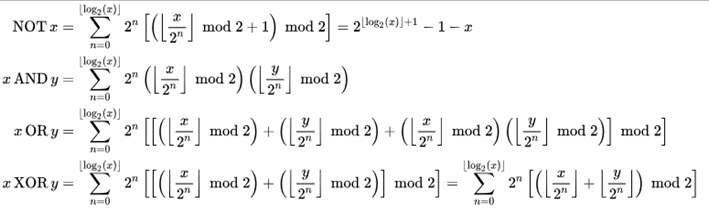
Some Useful Facts & Hacks:
Now some of the Facts and Hacks about these bitwise operators:
1. The bitwise operators should not be used in place of logical operators.
The result of logical operators (&&, || and !) is either 0 or 1, but bitwise operators return an integer value. Also, the logical operators consider any non-zero operand as 1. For example, consider the following program, the results of & and && are different for same operands.
int main()
{
int x = 2, y = 5;
(x & y)? printf(“True “) : printf(“False “);
(x && y)? printf(“True “) : printf(“False “);
return 0;
}
// Output: False True
2. The left-shift and right-shift operators are equivalent to multiplication and division by 2 respectively.
it works only if numbers are positive.
int main()
{
int x = 19;
printf (“x << 1 = %d\n”, x << 1);
printf (“x >> 1 = %d\n”, x >> 1);
return 0;
}
// Output: 38 9
3. The & operator can be used to quickly check if a number is odd or even.
The value of expression (x & 1) would be non-zero only if x is odd, otherwise the value would be zero.
int main()
{
int x = 19;
(x & 1)? printf(“Odd”): printf(“Even”);
return 0;
}
// Output: Odd
4. How to set a particular bit in a number:
If we want to set a bit at nth position in number ‘num’ ,it can be done using ‘OR’ operator( | ).
· First we left shift ‘1’ to n position via (1«n)
· Then, use ‘OR’ operator to set bit at that position.’OR’ operator is used because it will set the bit even if the bit is unset previously in binary representation of number ‘num’.
void set(int & num,int pos)
{
// First step is shift ‘1’, second
// step is bitwise OR
num |= (1 << pos);
}
int main()
{
int num = 4, pos = 1;
set(num, pos);
cout << (int)(num) << endl;
return 0;
}
Output:
6
5. How to unset/clear a bit at n’th position in a number:
Suppose we want to unset a bit at nth position in number ‘num’ then we have to do this with the help of ‘AND’ (&) operator.
· First we left shift ‘1’ to n position via (1«n) than we use bitwise NOT operator ‘~’ to unset this shifted ‘1’.
· Now after clearing this left shifted ‘1’ i.e making it to ‘0’ we will ‘AND’(&) with the number ‘num’ that will unset bit at nth position position.
void unset(int &num,int pos)
{
//Second step is to bitwise and this number with given number
num &= (~(1 << pos));
}
int main()
{
int num = 7;
int pos = 1;
unset(num, pos);
cout << num << endl;
return 0;
}
Output:
6
6. Toggling a bit at nth position:
Toggling means to turn bit ‘on’(1) if it was ‘off’(0) and to turn ‘off’(0) if it was ‘on’(1) previously. We will be using ‘XOR’ operator here which is this ‘^’. Process is same as above approach of shifting 1 by n bits and then xor operation with the number.
void toggle(int &num,int pos)
{
num ^= (1 << pos);
}
int main()
{
int num = 4;
int pos = 1;
toggle(num, pos);
cout << num << endl;
return 0;
}
Output:
6
7. Checking if bit at nth position is set or unset:
It is quite easily doable using ‘AND’ operator. Left shift ‘1’ to given position and then ‘AND’(‘&’).
bool at_position(int num,int pos)
{
bool bit = num & (1<<pos);
return bit;
}
int main()
{
int num = 5;
int pos = 0;
bool bit = at_position(num, pos);
cout << bit << endl;
return 0;
}
Output:
1
8. Inverting every bit of a number/1’s complement:
If we want to invert every bit of a number i.e change bit ‘0’ to ‘1’ and bit ‘1’ to ‘0’.We can do this with the help of ‘~’ operator. For example : if number is num=00101100 (binary representation) so ‘~num’ will be ‘11010011’. This is also the ‘1s complement of number’.
int main()
{
int num = 4;
// Inverting every bit of number num
cout << (~num);
return 0;
}
Output:
5
9. Two’s complement of the number:
2’s complement of a number is 1’s complement + 1.
So formally we can have 2’s complement by finding 1s complement and adding 1 to the result i.e (~num+1) or what else we can do is using ‘-‘ operator.
int main()
{
int num = 4;
int twos_complement = -num;
cout << “This is two’s complement “ << twos_complement << endl;
cout << “This is also two’s complement “ << (~num+1) << endl;
return 0;
}
Output:
This is two’s complement -4
This is also two’s complement -4
10. Stripping off the lowest set bit :
In many situations we want to strip off the lowest set bit for example in Binary Indexed tree data structure, counting number of set bit in a number.
We do something like this:
X = X & (X-1)
But how does it even work ?
Let us see this by taking an example, let X = 1100.
(X-1) inverts all the bits till it encounter lowest set ‘1’ and it also invert that lowest set ‘1’.
X-1 becomes 1011. After ‘ANDing’ X with X-1 we get lowest set bit stripped.
void strip_last_set_bit(int &num)
{
num = num & (num-1);
}
int main()
{
int num = 7;
strip_last_set_bit(num);
cout << num << endl;
return 0;
}
Output:
6
11. Getting lowest set bit of a number:
This is done by using expression ‘X &(-X)’Let us see this by taking an example: Let X = 00101100. So ~X(1’s complement) will be ‘11010011’ and 2’s complement will be (~X+1 or -X) i.e ‘11010100’.
So if we ‘AND’ original number ‘X’ with its two’s complement which is ‘-X’, we get lowest set bit.
00101100
& 11010100
— — — — — -
00000100
int lowest_set_bit(int num)
{
int ret = num & (-num);
return ret;
}
int main()
{
int num = 10;
int ans = lowest_set_bit(num);
cout << ans << endl;
return 0;
}
Output:
2
12. Clear all bits from LSB to ith bit:
Assumption:
· 0 based indexing of bits from left to right.
· Setting i-th bit means, turning i-th bit to 1
· Clearing i-th bit means, turning i-th bit to 0
mask = ~ ((1 << i+1 ) — 1); x &= mask;
Logic: To clear all bits from LSB to i-th bit, we have to AND x with mask having LSB to i-th bit 0. To obtain such mask, first left shift 1 i times. Now if we minus 1 from that, all the bits from 0 to i-1 become 1 and remaining bits become 0. Now we can simply take complement of mask to get all first i bits to 0 and remaining to 1.
Example- x = 29 (00011101) and we want to clear LSB to 3rd bit, total 4 bits mask -> 1 << 4 -> 16(00010000) Mask -> 16–1 -> 15(0000####) mask -> ~mask -> ####0000 x & mask -> 16 (00010000)
13. Clearing all bits from MSB to i-th bit:
mask = (1 << i) — 1; x &= mask;
Logic: To clear all bits from MSB to i-th bit, we have to AND x with mask having MSB to i-th bit 0. To obtain such mask, first left shift 1 i times. Now if we minus 1 from that, all the bits from 0 to i-1 become 1 and remaining bits become 0.
Example- x = 215 (11010111) and we want to clear MSB to 4th bit, total 4 bits mask -> 1 << 4 -> 16(00010000) mask -> 16–1 -> 15(0000####) x & mask -> 7(00000111)
14. Upper case English alphabet to lower case:
ch |= ‘ ‘; Logic: The bit representation of upper case and lower case English alphabets are –
A -> 01000001 a -> 01100001 B -> 01000010 b -> 01100010 C -> 01000011 c -> 01100011 . . Z -> 01011010 z -> 0####010
As we can see if we set 5th bit of upper case characters, it will be converted into lower case character. We have to prepare a mask having 5th bit 1 and other 0 (00100000). This mask is bit representation of space character (‘ ‘). The character ‘ch’ then ORed with mask.
Example-
ch = ‘A’ (01000001) mask = ‘‘ (00100000) ch | mask = ‘a’ (01100001)
Please refer Case conversion (Lower to Upper and Vice Versa) for details.
15. Lower case English alphabet to upper case:
ch &= ‘_’ ; Logic: The bit representation of upper case and lower case English alphabets are –
A -> 01000001 a -> 01100001 B -> 01000010 b -> 01100010 C -> 01000011 c -> 01100011 . . . . Z -> 01011010 z -> 0####010
As we can see if we clear 5th bit of lower case characters, it will be converted into upper case character. We have to prepare a mask having 5th bit 0 and other 1 (10####11). This mask is bit representation of underscore character (‘_‘). The character ‘ch’ then AND with mask.
Example-
ch = ‘a’ (01100001) mask = ‘_ ‘ (110####1) ch | mask = ‘A’ (01000001)
Please refer Case conversion (Lower to Upper and Vice Versa) for details.
16. Count set bits in integer:
int countSetBits(int x)
{
int count = 0;
while (x)
{
x &= (x-1);
count++;
}
return count;
}
Logic: This is Brian Kernighan’s algorithm.
17. Find log base 2 of 32 bit integer:
int log2(int x)
{
int res = 0;
while (x >>= 1)
res++;
return res;
}
Logic: We right shift x repeatedly until it becomes 0, meanwhile we keep count on the shift operation. This count value is the log2(x).
18. Checking if given 32 bit integer is power of 2:
int isPowerof2(int x)
{
return (x && !(x & x-1));
}
Logic: All the power of 2 have only single bit set e.g. 16 (00010000). If we minus 1 from this, all the bits from LSB to set bit get toggled, i.e., 16–1 = 15 (0000####). Now if we AND x with (x-1) and the result is 0 then we can say that x is power of 2 otherwise not. We have to take extra care when x = 0.
Example
x = 16(000100000) x — 1 = 15(0000####) x & (x-1) = 0 so 16 is power of 2
Bits Manipulation:
1. Compute XOR from 1 to n (direct method) :
// Direct XOR of all numbers from 1 to n
int computeXOR(int n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
Input: 6
Output: 7
Proof: If you try the naive approach upto 12 on paper then you will notice that before every multiple of 4 the answer becomes 0.
Number Binary-Repr XOR-from-1-to-n
1 1 [0001] 2 10 [0011] 3 11 [0000] ← — — We get a 0 4 100 [0100] ← — — Equals to n 5 101 [0001] 6 110 [0111] 7 111 [0000] ← — — We get 0 8 1000 [1000] ← — — Equals to n 9 1001 [0001] 10 1010 [1011] 11 1011 [0000] ← — — We get 0 12 1100 [1100] ← — — Equals to n
2. We can quickly calculate the total number of combinations with numbers smaller than or equal to with a number whose sum and XOR are equal. Instead of using looping (Brute force method), we can directly find it by a mathematical trick i.e.
Answer = pow(2, count of zero bits) Proof:Since we know a + b = a ^ b + 2 * (a & b)
We can write, n + i = n ^ i + 2 * (n & i)
So n + i = n ^ i implies n & i = 0
Hence our problem reduces to finding values of i such that n & i = 0. How to find count of such pairs? We can use the count of unset-bits in the binary representation of n. For n & i to be zero, i must unset all set-bits of n. If the kth bit is set at a particular in n, kth bit in i must be 0 always, else kth bit of i can be 0 or 1
Hence, total such combinations are 2^(count of unset bits in n)
3. Find XOR of all subsets of a set. We can do it in O(1) time. The answer is always 0 if given set has more than one elements. For set with single element, the answer is value of single element.
Proof:The logic goes simple. Let us consider n’th element, it can be included in all subsets of remaining (n-1) elements. The number of subsets for (n-1) elements is equal to 2(n-1) which is always even when n>1. Thus, in the XOR result, every element is included even number of times and XOR of even occurrences of any number is 0.
4. We can quickly find number of leading, trailing zeroes and number of 1’s in a binary code of an integer in C++ using GCC. It can be done by using inbuilt function i.e.
Number of leading zeroes: builtin_clz(x) Number of trailing zeroes : builtin_ctz(x) Number of 1-bits: __builtin_popcount(x) Refer GCC inbuilt functions for details.
5. Convert binary code directly into an integer in C++.
// Conversion into Binary code//
int main()
{
auto number = 0b011;
cout << number;
return 0;
}
Output: 3
6. The Quickest way to swap two numbers:
a ^= b; b ^= a; a ^= b;
Refer swap two numbers for details.
7. Simple approach to flip the bits of a number: It can be done by a simple way, just simply subtract the number from the value obtained when all the bits are equal to 1 .
Number : Given Number Value : A number with all bits set in given number. Flipped number = Value — Number.
Example :
Number = 23, Binary form: 10111; After flipping digits number will be: 01000; Value: ####1 = 31;
8. We can find the most significant set bit in O(1) time for a fixed size integer. For example below code is for 32 bit integer.
int setBitNumber(int n)
{
// Below steps set bits after
// MSB (including MSB)
// Suppose n is 273 (binary
// is 100010001). It does following
// 100010001 | 010001000 = 110011001
n |= n>>1;
// This makes sure 4 bits
// (From MSB and including MSB)
// are set. It does following
// 110011001 | 001100110 = ########1
n |= n>>2;
n |= n>>4;
n |= n>>8;
n |= n>>16;
// Increment n by 1 so that
// there is only one set bit
// which is just before original
// MSB. n now becomes 1000000000
n = n + 1;
// Return original MSB after shifting.
// n now becomes 100000000
return (n >> 1);
}
Refer Find most significant set bit of a number for details.
9. We can quickly check if bits in a number are in alternate pattern (like 101010). We compute n ^ (n » 1). If n has an alternate pattern, then n ^ (n » 1) operation will produce a number having set bits only. ‘^’ is a bitwise XOR operation.
That covered most of the application of Bitwise operators. For more amazing things that can be done using Bitwise operators refer to this Quora answer. And comment below if you think something needs to be corrected or if you like it.
You can find PDF version here.
References: